열심히 끝까지
18강 배열 - 메서드 오버로딩 본문
<복습>
메서드
정의 : 여러 명령들을 나열한 묶음
사용이유 ? 이름 호출하는 것으로 여러 개의 명령을 한번에 실행
구조
<구현부>
메서드가 어떤 명령들로 구성이 되어 있는지 구현하는 부분
리턴타입 메서드명(매개변수1, 매개변수2){
명령 1;
명령 2;
명령 3;
return 리턴값;
}
리턴타입 : void -> 리턴값이 존재하지 않는다.
-------------------------
<호출부>
메서드에 구현된 명령들이 실행 될 수 있도록 호출하는 부분
메서드명(값1, 값2);
18-1 ) 메서드 오버로딩
(1) 오버로딩의 정의
: 오버로딩(Overloading)은 매개변수의 개수와 타입은 다르지만
이름이 같은 메서드를 여러 개 정의하는 것
- 로딩 : 메모리에 적재하다
- 오버로딩 : 메서드 중복 정의
- 일반적으로 메서드 사용시, 메서드명을 구분해서 사용
- 하지만, 같은 기능을 갖고 있는 메서드라면, 매번 이름 정의하는 것이 불필요
*****
컴퓨터가 함수를 구분하는 시그니처
1. 함수명
2. 함수의 매개변수의 개수
3. 함수의 매개변수의 타입
-----------------------------------------------
2 + 3 = 5 정수 + 정수
1.23 + 3.12 = 4.35 실수 + 실수
"A" + "B" = "AB" 문자열+ 문자열


sum(2, 3)
sum(1.23, 3.14)
sum("A", "B)
이 위의 것이 지원되지 않는다하면..?
sum_int(2, 3)
sum_double(1.23, 3.14)
sum_String("A", "B)
(2) 오버로딩 방법
ex )

1. 정수형 값을 두 개 전달받아 두 수의 합을 출력하는 메서드 구현
static void sum(int x, int y) {
System.out.println( x + y );
}
2. 실수형 값을 두 개 전달받아 두 수의 합을 출력하는 메서드 구현
ststic void sum(double x, double y) {
System.out.println( x + y );
}
3. 정수형 값을 세 개를 전달받아 세 수의 합을 출력하는 메서드 구현
static void sum(int x, int y, int z) {
System.out.println( x + y + z );
}
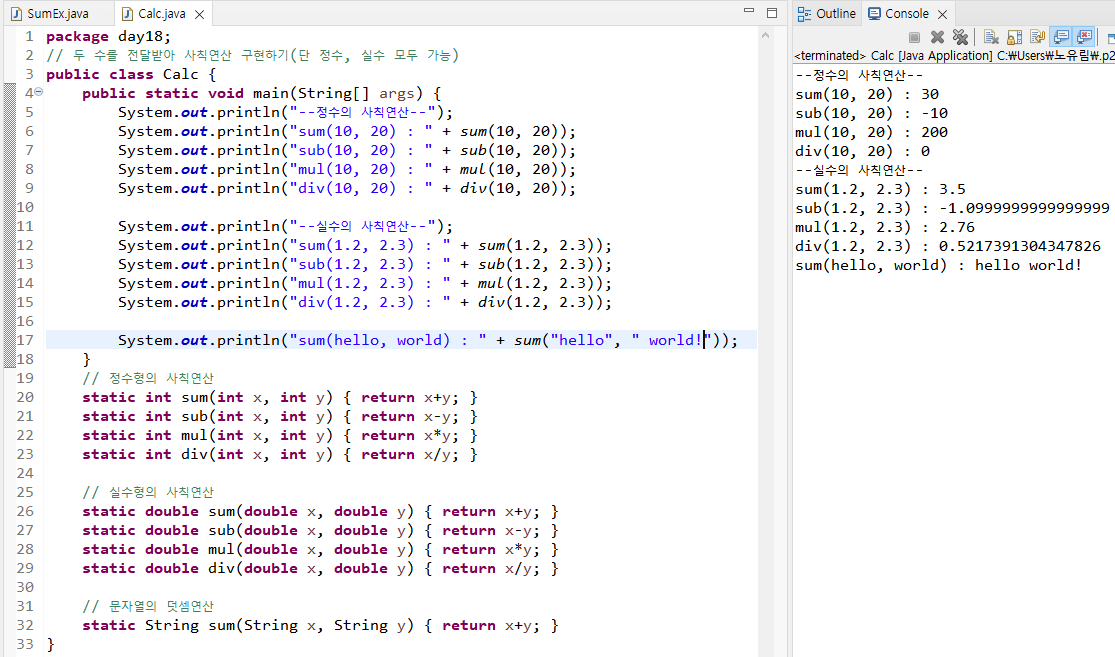
< 실습 > Calc.java
두 수를 전달받아, 두 수의 +, -, *, / 을 계산하는 메서드를 만들어라
단, 입력받은 수는 정수, 실수 모두 가능!
--------------------------
<실수의 오류>
컴퓨터는 실수값을 정확하게 표현할 수 없다
=> 유한한 개수의 비트를 가지고
무한한 실수를 표현을 해야하므로,
- 1.1이 나오는 것이 아니라 가장 근사한 근사값이 나온다
'멘토씨리즈 JAVA' 카테고리의 다른 글
| 20강 클래스에 대하여 - 클래스와 객체 (0) | 2022.04.28 |
|---|---|
| 19강 클래스에 대하여 - 객체지향언어 (0) | 2022.04.28 |
| 17강 배열 - 메서드 / 접근제한자 리턴타입 매개변수 (0) | 2022.04.27 |
| 16강 배열 - 연습 / 카페주문 프로그램 제작 (0) | 2022.04.26 |
| 15강 배열 - 배열의 복제 및 foreach문 (0) | 2022.04.26 |
